Find the container with most water (Blind 75) — O(n) Solution

Problem Overview

We are given an array heights of size n. The value at each index represents the height of a vertical bar.

We need to find two bars such that together they can hold the maximum amount of water.

Note: We are not allowed to slant the container.

LeetCode - Container With Most Water

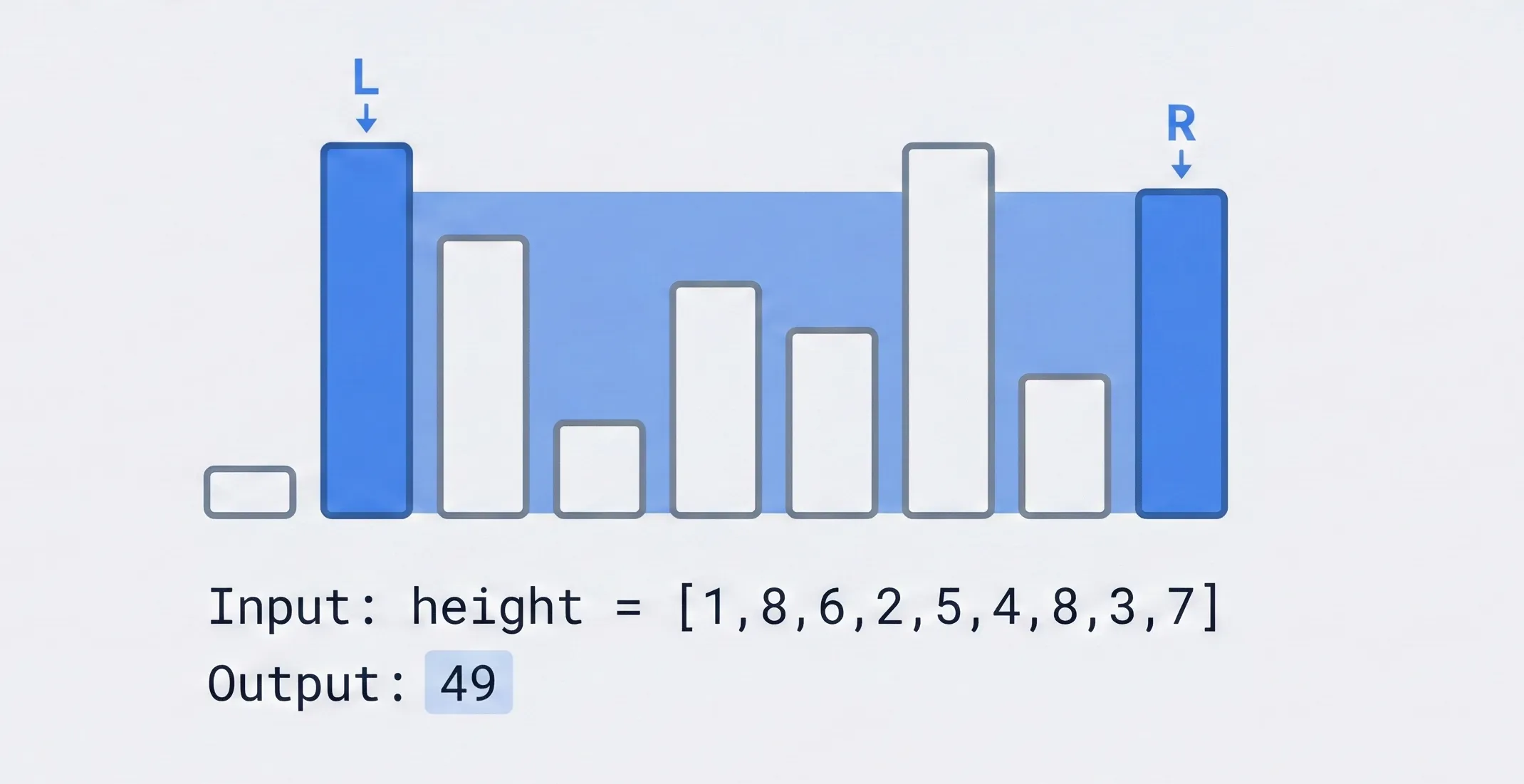
Example

Input: height = [1,8,6,2,5,4,8,3,7]
Output: 49

Greedy Logic Attempt

The idea was inspired by Kadane’s Algorithm

• Track maximum height so far.
• Compute area at every step.
• Maintain maxSoFar.

Code Attempt

class Solution {
public:
    int maxArea(vector<int>& height) {

        int maxHeight = 0;
        int maxIndex = 0;
        int maxSoFar = 0;

        int n = height.size();
      
        for(int i=0;i<n;i++){
            
            if(maxHeight < height[i]){
                maxHeight = height[i];
                maxIndex = i;
            }

            maxSoFar = min(maxHeight, height[i]) * (i-maxIndex);
        }

        return maxSoFar;
        
    }
};

Why This Fails

The container area depends on height and width:

• Height → min(height[i], height[j])
• Width → j - i

Problems with the greedy approach:

• We fixed one side of the height.
• A slightly smaller height with much larger width can produce a bigger area.
• Not all valid pairs are checked.

Optimal Solution – Two Pointer Approach

Idea:

• Start one pointer at the beginning (l = 0)
• Start the other at the end (r = n - 1)
• Calculate area at each step
• Move the pointer that has the smaller height

Why Move the Smaller Height?

• Area formula: Area = min(height[l], height[r]) * (r - l)

• The smaller height is the limiting factor.

• Moving the taller height won’t help because:

  • Width decreases
  • Height limit doesn’t improve

• Only moving the smaller height gives a chance of finding a taller boundary

Code – Two Pointer Approach

class Solution {
public:
    int maxArea(vector<int>& height) {

        int maxSoFar = 0;
        int n = height.size();

        int l = 0, r = n - 1;

        while (l < r) {

            int area = min(height[l], height[r]) * (r - l);

            maxSoFar = max(maxSoFar, area);

            if (height[l] < height[r]) {
                l++;
            } else {
                r--;
            }
        }

        return maxSoFar;
    }
};

Time and Space Complexity

• Time: O(n)
• Space: O(1)

Final Takeaways

• Maximum area is not only about maximum height.
• Width plays an equally important role.
• When a problem involves two boundaries and width between them, think about two pointers.
• Failed attempts are not wasted — they help you understand constraints better.