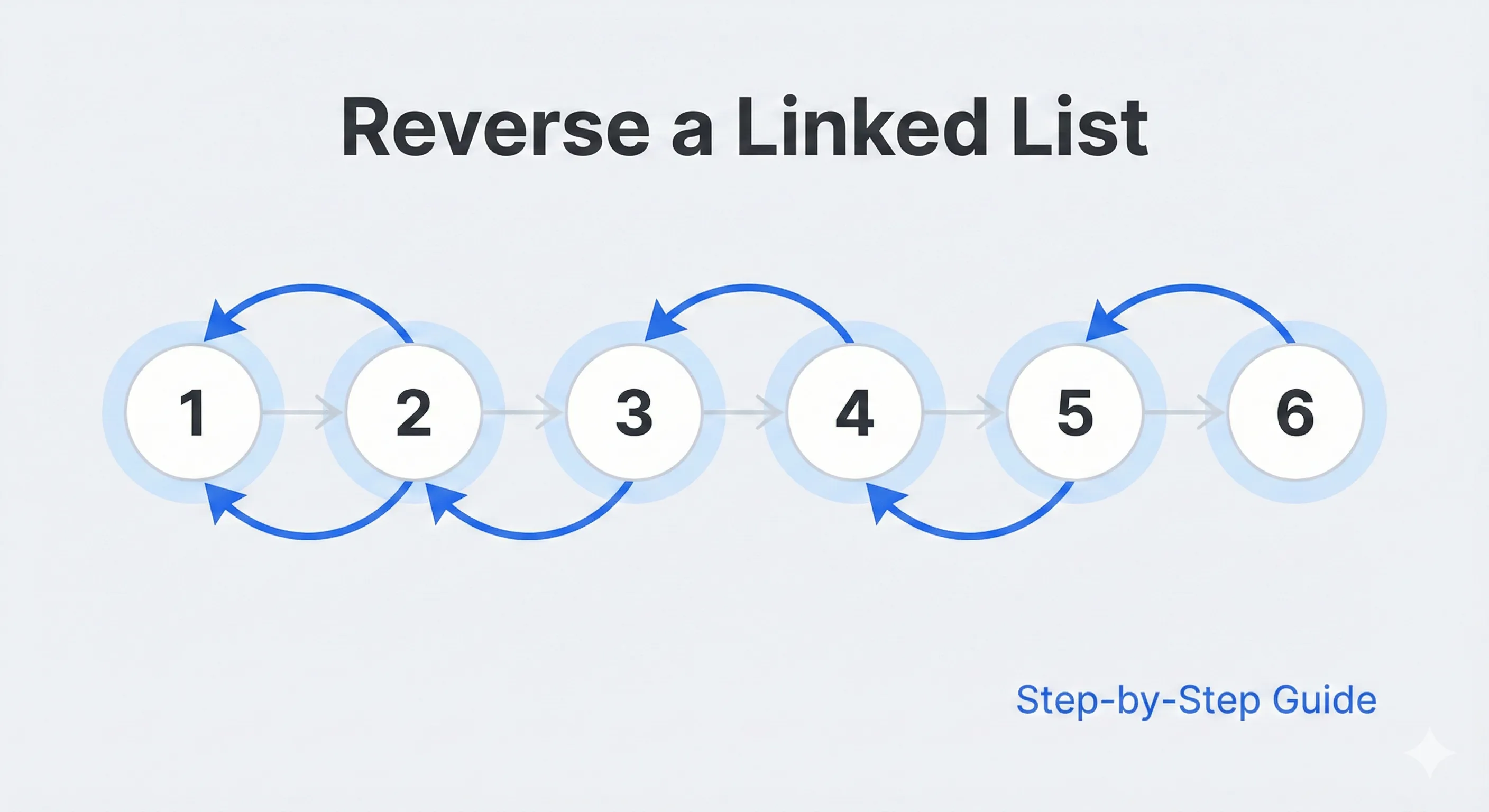
Problem Overview
We are given the head of a singly linked list. We need to reverse the linked list.
Follow-up: Solve it iteratively and recursively.
Example
Input: head = [1,2,3,4,5]
Output: [5,4,3,2,1]
Key Observations
- In a singly linked list, we can only traverse forward.
- Each node contains a pointer to the next node.
- Reversing the list means changing the direction of every
nextpointer. - We must carefully store the next node before modifying links.
Approach 1: Brute Force (Using Stack)
Intuition
- Traverse the list.
- Push every node onto a stack.
- Pop nodes one by one to rebuild the list in reverse order.
Code
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if (!head)
return NULL;
stack<ListNode*> st;
ListNode* curr = head;
while (curr != NULL) {
st.push(curr);
curr = curr->next;
}
ListNode* newHead = st.top();
st.pop();
curr = newHead;
while (!st.empty()) {
curr->next = st.top();
st.pop();
curr = curr->next;
}
curr->next = NULL;
return newHead;
}
};
Why It Is Not Optimal
- Uses extra data structure (stack).
- Requires additional memory.
- The problem can be solved in-place.
Time and Space Complexity
- Time: O(n)
- Space: O(n)
Approach 2: Three Pointer (Optimal Iterative)
Intuition
We maintain three pointers:
prev→ previous nodecurr→ current nodenext→ next node
At each step:
- Store
next. - Reverse the link (
curr->next = prev). - Move all pointers forward.
Dry Run (First Two Iterations)
Initial State
NULL <- 1 -> 2 -> 3 -> 4 -> 5
prev curr
Iteration 1
next = curr->next; // 2
curr->next = prev; // 1 -> NULL
prev = curr; // prev = 1
curr = next; // curr = 2
State:
NULL <- 1 2 -> 3 -> 4 -> 5
prev curr
Iteration 2
next = curr->next; // 3
curr->next = prev; // 2 -> 1
prev = curr; // prev = 2
curr = next; // curr = 3
State:
NULL <- 1 <- 2 3 -> 4 -> 5
prev curr
Continue until curr == NULL.
Return prev since it becomes the new head.
Code (Optimal Iterative)
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode* curr = head;
ListNode* prev = NULL;
while (curr) {
ListNode* next = curr->next;
curr->next = prev;
prev = curr;
curr = next;
}
return prev;
}
};
Time & Space Complexity (Iterative)
- Time: O(n)
- Space: O(1)
Approach 3: Recursive
Intuition
- This follows the same logic as the iterative approach.
- Instead of looping, recursion moves forward until the end.
prevtracks the reversed portion.- When
currbecomesNULL, returnprev(new head).
Code
class Solution {
public:
ListNode* reverseList(ListNode* head) {
return nodeReverse(head, NULL);
}
ListNode* nodeReverse(ListNode* curr, ListNode* prev) {
if (!curr)
return prev;
ListNode* next = curr->next;
curr->next = prev;
return nodeReverse(next, curr);
}
};
Time and Space Complexity (Recursive)
- Time: O(n)
- Space: O(n) // recursion stack
Edge Cases
- Empty list → return NULL.
- Single node → return the same node.
- Very large list → recursive solution may cause stack overflow.
Final Takeaways
- Always store
nextbefore modifyingcurr->next. - Pointer update order matters.
- Return
prev, nothead. - Iterative solution is optimal in interviews.
- Recursive solution is clean but uses extra stack space.