Rotate Image (Blind 75): 90° Matrix Rotation Explained

Problem Overview

• We are given a 2D matrix of size n * n.
• The matrix represents an image.
• Our goal is to rotate the image by 90 degrees clockwise.
• The solution must use constant extra space (in-place).

LeetCode - Rotate Image

Example

Input:
matrix = [[1,2,3],
          [4,5,6],
          [7,8,9]]

Output:
[[7,4,1],
 [8,5,2],
 [9,6,3]]

Intuition

If we remember basic matrix properties:

• Transpose of a matrix
• Reverse of each row

If we:

1. First take the transpose (swap (i,j) with (j,i))
2. Then reverse every row

We effectively rotate the matrix 90° clockwise.

Why this works:

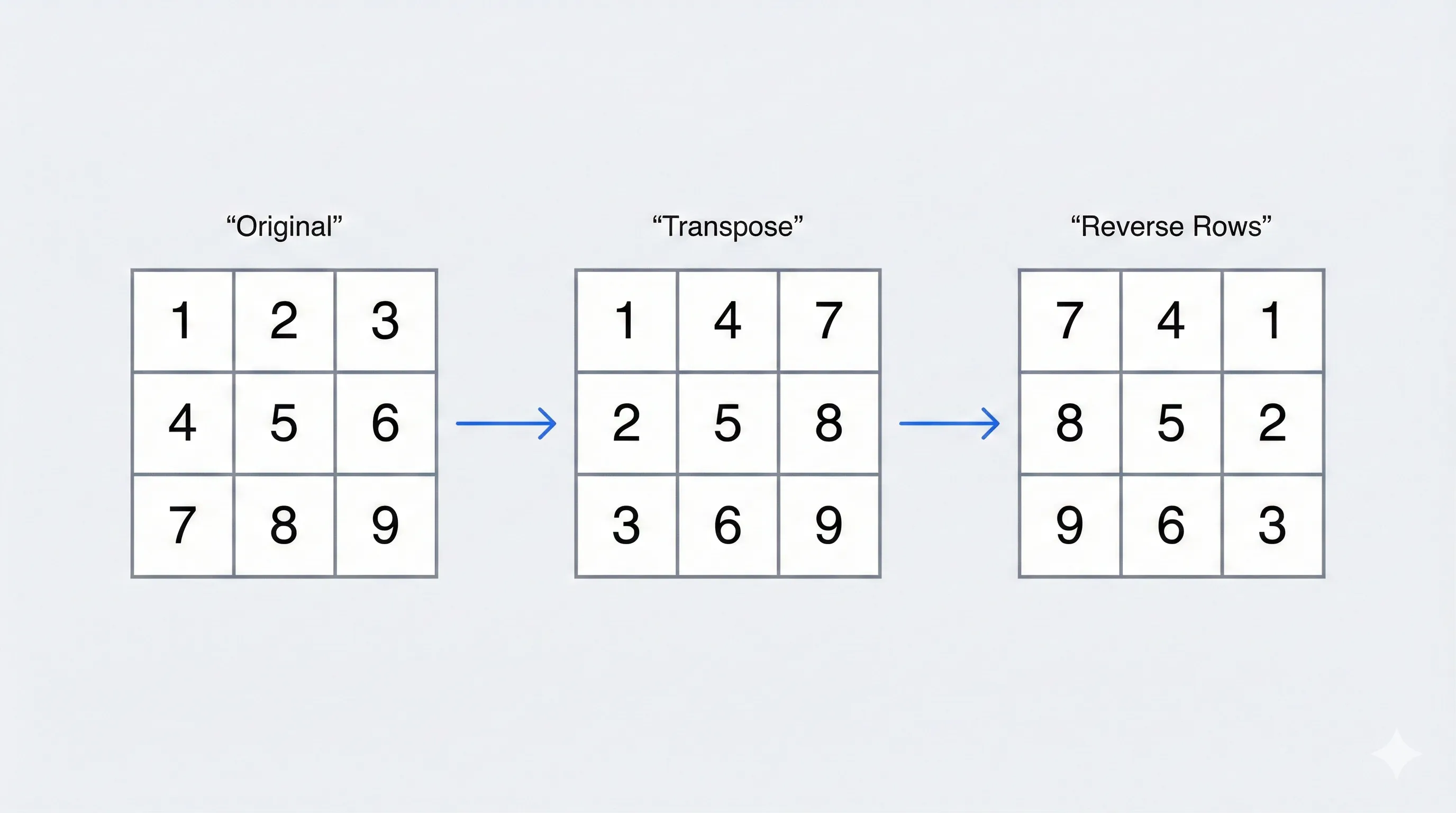
This is exactly a 90° clockwise rotation.

Approach

Step 1 — Transpose the Matrix

Swap:

matrix[i][j] ↔ matrix[j][i]

Important:

• Start j from i.
• Otherwise you will swap elements twice.

Step 2 — Reverse Each Row

• Reverse only half of each row.

Edge Case:

• If we reverse the entire row twice, we get the original matrix.
• So only iterate till n/2.

Optimal Solution

Code — Two Pointer Approach

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {

        int n = matrix.size();

        // Step 1: Transpose
        for (int i = 0; i < n; i++) {
            for (int j = i; j < n; j++) {
                swap(matrix[i][j], matrix[j][i]);
            }
        }

        // Step 2: Reverse each row
        for (int i = 0; i < n; i++) {

            int l = 0, r = n - 1;

            while (l < r) {
                swap(matrix[i][l], matrix[i][r]);
                l++;
                r--;
            }
        }
    }
};

Code — Using Nested Loops

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {

        int n = matrix.size();

        // Transpose
        for (int i = 0; i < n; i++) {
            for (int j = i; j < n; j++) {
                swap(matrix[i][j], matrix[j][i]);
            }
        }

        // Reverse each row
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n / 2; j++) {
                swap(matrix[i][j], matrix[i][n - 1 - j]);
            }
        }
    }
};

Time & Space Complexity

• Time: O(n²)

  • Transpose → O(n²)
  • Reverse → O(n²)

• Space: O(1)

Final Takeaway

• Knowing matrix properties (like transpose) simplifies problems.
• Many in-place matrix transformations are combinations of smaller operations.