Problem Overview

We are given a sorted array nums of distinct integers The array has been possibly rotated at some pivot k (unknown).

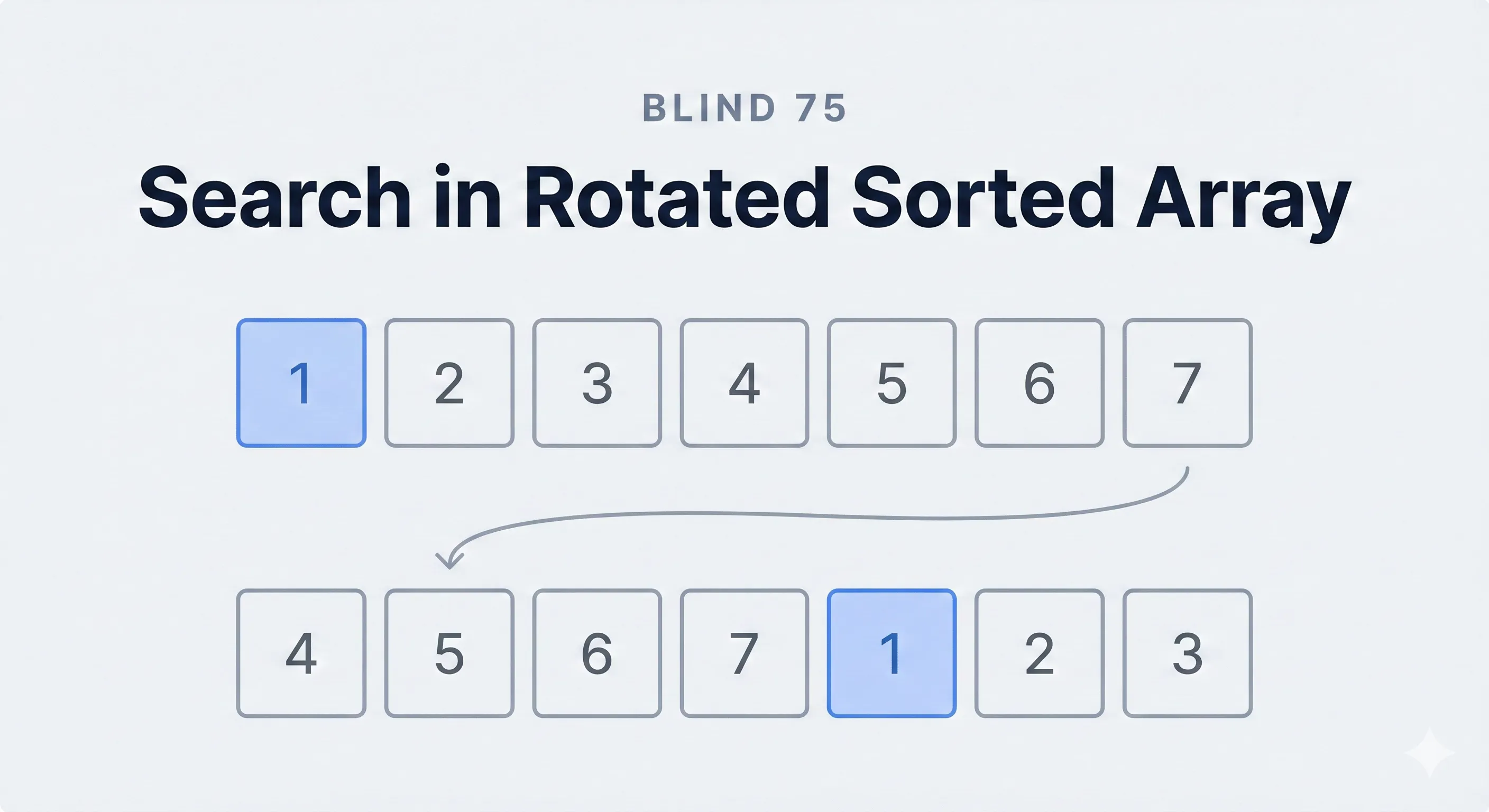
Example:

Original: [0,1,2,4,5,6,7]
Rotated : [4,5,6,7,0,1,2]

We must return the index of target if it exists in the array else return -1.

The required time complexity is O(log n).

LeetCode - Search in Rotated Sorted Array

Brute Force Approach

The simplest approach is to scan the entire array.

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int n = nums.size();

        for (int i = 0; i < n; i++) {
            if (nums[i] == target) {
                return i;
            }
        }

        return -1;
    }
};

Why This Fails

  • Linear search takes O(n)
  • The problem explicitly requires O(log n)
  • Therefore, we must use Binary Search

Key Observations

Even though the array is rotated:

  • It was originally sorted.
  • Rotation does not destroy sorted order completely.
  • At least one half of the array is always sorted.

This is the core insight.

If we can:

  1. Identify the sorted half
  2. Check whether the target lies inside that half

We can eliminate half the array in each step achieving O(log n).

The problem is similar to find minimum in sorted rotated array

We apply binary search with an additional check to determine which half is sorted.

Steps

  1. Initialize:

    • left = 0
    • right = n - 1

  2. While left <= right:

    • Compute mid
    • If nums[mid] == target → return mid

  3. Determine which half is sorted:

    • If nums[left] <= nums[mid]

      • Left half is sorted

    • Otherwise

      • Right half is sorted

  4. Check if target lies inside the sorted half:

    • If yes → search inside that half
    • If no → search in the other half

The main idea here is to eliminate one half of the array at each iteration

Code (C++)

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0, right = nums.size() - 1;

        while (left <= right) {
            int mid = left + (right - left) / 2;

            if (nums[mid] == target)
                return mid;

            if (nums[left] <= nums[mid]) { 
                // Left half is sorted
                if (target >= nums[left] && target < nums[mid])
                    right = mid - 1;
                else
                    left = mid + 1;
            } else {
                // Right half is sorted
                if (target > nums[mid] && target <= nums[right])
                    left = mid + 1;
                else
                    right = mid - 1;
            }
        }

        return -1;
    }
};

Time & Space Complexity

  • Time: O(log n)
  • Space: O(1)

Final Takeaways

  • Always read constraints carefully — time complexity hints often reveal the intended approach.
  • Rotated sorted array problems almost always rely on identifying a sorted half.