Spiral Matrix (Blind 75): Matrix traversal in spiral order

Problem Overview

• We are given a matrix of size m * n.
• We need to return all elements of the matrix in spiral order.
• Note: The matrix is not necessarily square.

LeetCode - Spiral Matrix

Example

Input: matrix = [[1,2,3],
                 [4,5,6],
                 [7,8,9]]

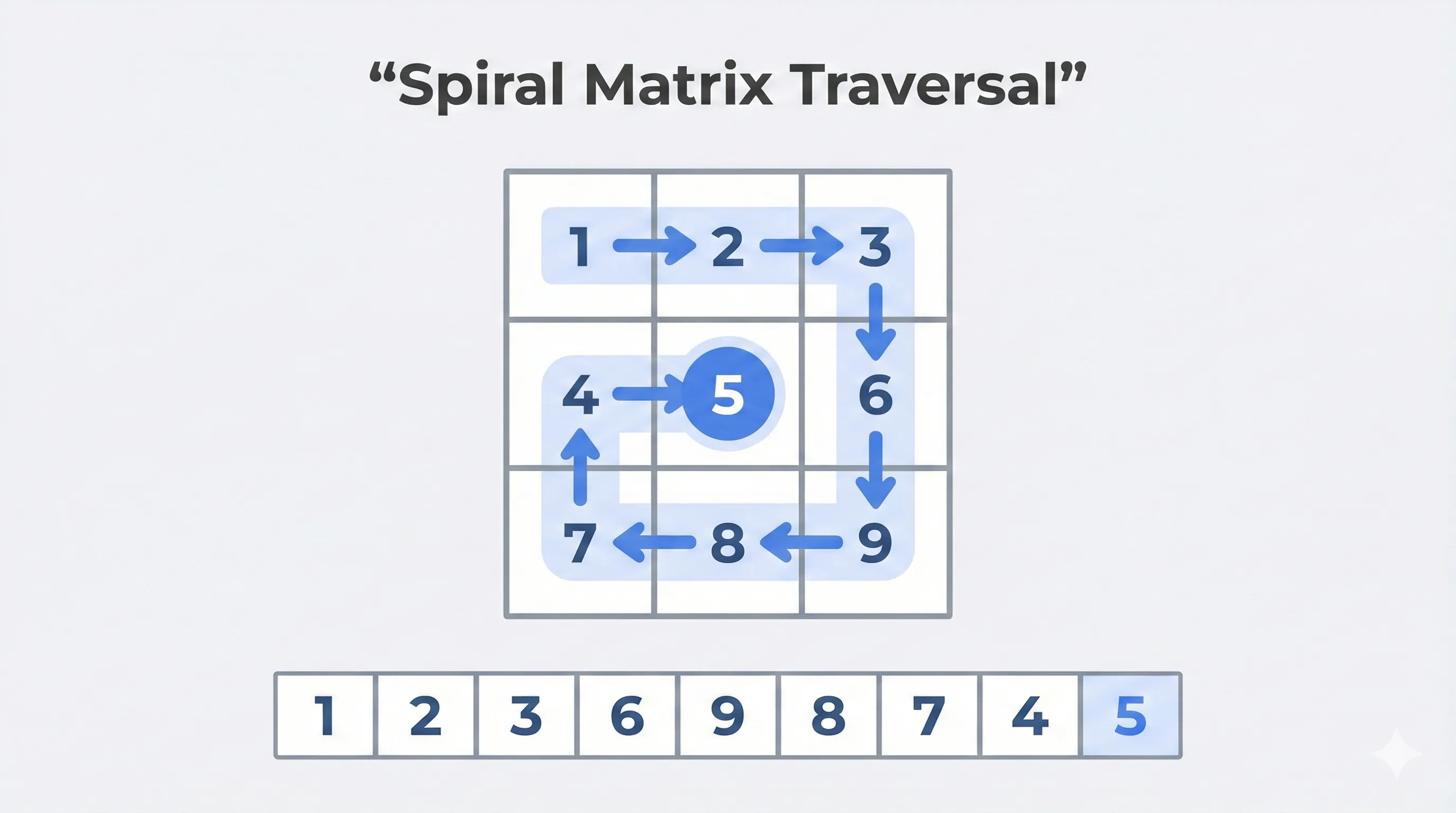
Output: [1,2,3,6,9,8,7,4,5]

Intuition

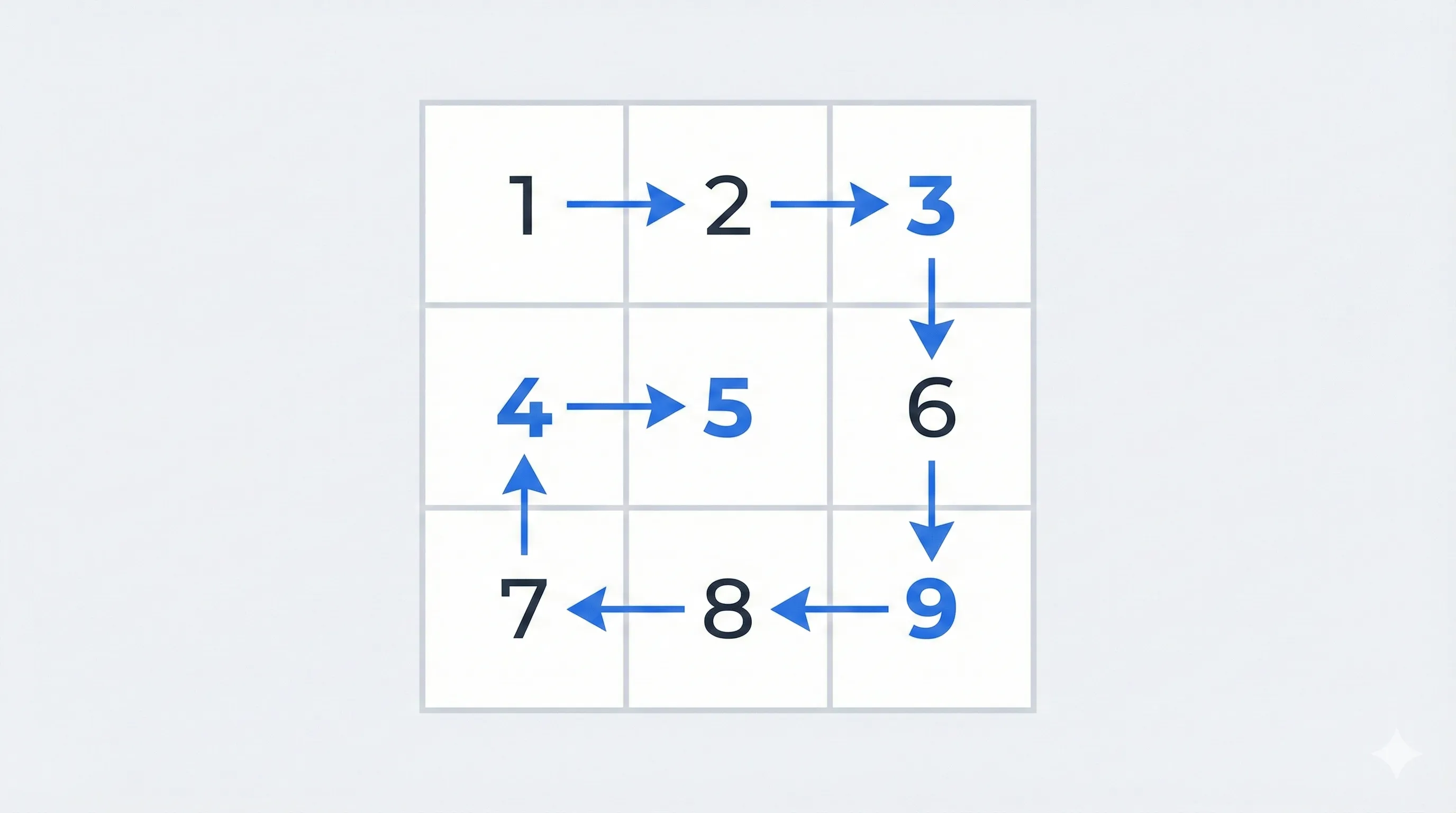
We need to travese the matrix in this order

Indices traversal:

(0,0) → (0,1) → (0,2)          right
(0,2) ↓ (1,2) ↓ (2,2)          down
(2,2) ← (2,1) ← (2,0)          left
(2,0) ↑ (1,0)                  up
(1,0) → (1,1)                  right

So the movement pattern becomes:

(top, left)    → (top, right)     | move right
(top, right)   → (bottom, right)  | move down
(bottom, right)→ (bottom, left)   | move left
(bottom, left) → (top, left)      | move up

Observation:

• If we repeat this pattern and shrink the boundaries after each cycle, we can cover the entire matrix.

Optimal Solution

Approach

• Maintain four boundaries:

  • top
  • bottom
  • left
  • right

• At every iteration:

  1. Move left → right (top row)
  2. Move top → bottom (right column)
  3. Move right → left (bottom row)
  4. Move bottom → top (left column)

• After each direction, shrink the corresponding boundary.

Important Edge Cases

• Always check:

  • top <= bottom
  • left <= right

• Reason: After shrinking, an extra invalid iteration can happen.

• Without these checks, elements may get duplicated.

Code Implementation

class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {

        int m = matrix.size();
        int n = matrix[0].size();

        vector<int> result;

        int top = 0, left = 0;
        int right = n - 1, bottom = m - 1;

        while (left <= right && top <= bottom) {

            // Move left to right
            for (int col = left; col <= right; col++) {
                result.push_back(matrix[top][col]);
            }
            top++;

            // Move top to bottom
            for (int row = top; row <= bottom; row++) {
                result.push_back(matrix[row][right]);
            }
            right--;

            // Edge Case Check
            if (top <= bottom) {
                // Move right to left
                for (int col = right; col >= left; col--) {
                    result.push_back(matrix[bottom][col]);
                }
                bottom--;
            }

            // Edge Case Check
            if (left <= right) {
                // Move bottom to top
                for (int row = bottom; row >= top; row--) {
                    result.push_back(matrix[row][left]);
                }
                left++;
            }
        }

        return result;
    }
};

Time and Space Complexity

• Time: O(m * n)

  • Every element is visited exactly once.

• Space: O(1) extra

  • The output array is not counted.

Final Takeaways

• Break the problem into smaller steps.
• Edge condition checks (top <= bottom, left <= right) are critical to avoid duplicates.
• This approach works for non-square matrices too.