Problem Overview

  • We are given a 2D array of characters named board.
  • The board size is m x n.
  • We are also given a string word.
  • Our goal is to find whether the word exists in the board.
  • If found → return true, otherwise → return false.

LeetCode - Word Search

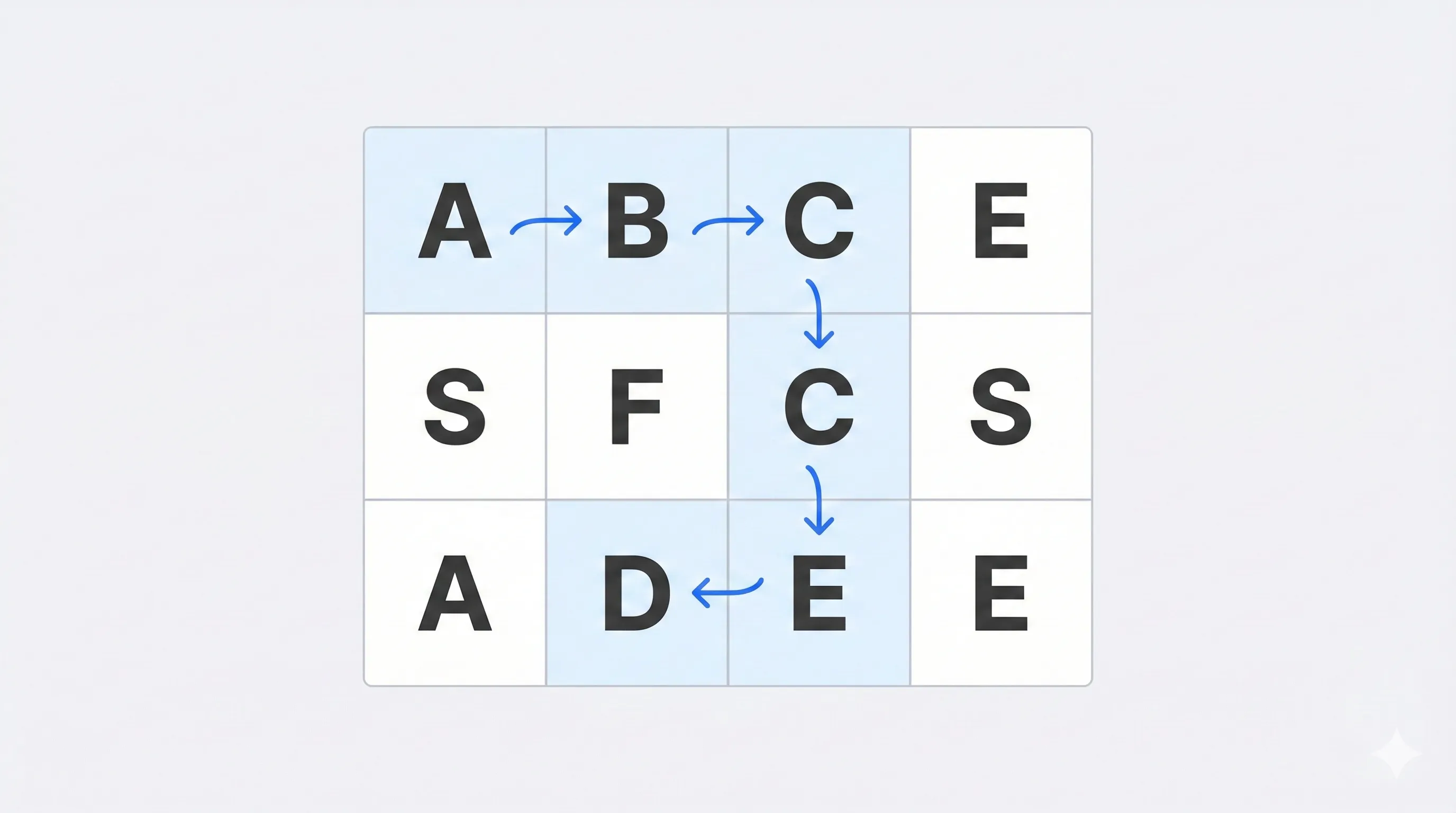
Example

Input: board = [["A","B","C","E"],
                ["S","F","C","S"],
                ["A","D","E","E"]],
       word = "ABCCED"

Output: true

Visual representaiton of travesal in matrix to search the word

Intuition

  • First, we need to find word[0] in the matrix.

  • If we find it, we start searching in four directions using recurrsion

    • Top
    • Bottom
    • Left
    • Right

  • From there, we search for the next character.

  • If it matches, we continue recursively.

  • If we reach the last character → return true.

This problem is combination DFS and Backtracking .

Approach

Base Solution — DFS + Backtracking

class Solution {
public:
    bool exist(vector<vector<char>>& board, string word) {

        int m = board.size();
        int n = board[0].size();

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (search(i, j, board, word, 0))
                    return true;
            }
        }

        return false;
    }

    bool search(int i, int j, vector<vector<char>>& board,
                string& word, int index) {

        int m = board.size();
        int n = board[0].size();

        // Boundary check
        if (i < 0 || i >= m || j < 0 || j >= n)
            return false;

        // Character mismatch
        if (board[i][j] != word[index])
            return false;

        // If last character matched
        if (index == word.size() - 1)
            return true;

        char temp = board[i][j];
        board[i][j] = '#';   // mark visited

        bool found =
            search(i+1, j, board, word, index+1) ||
            search(i-1, j, board, word, index+1) ||
            search(i, j+1, board, word, index+1) ||
            search(i, j-1, board, word, index+1);

        board[i][j] = temp;  // restore (backtrack)

        return found;
    }
};

Optimized Version

What We Improve

  1. Frequency Pruning

    • If the board does not contain required characters → return false early.
    • This avoids unnecessary recursion.

  2. Start from the Rarer Character

    • If the last character appears less frequently than the first character,
    • Reverse the word.
    • This reduces branching and recursion calls.

Optimized Code

class Solution {
public:
    bool exist(vector<vector<char>>& board, string word) {

        int m = board.size();
        int n = board[0].size();

        // Step 1: Frequency pruning
        vector<int> boardFreq(128, 0);
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                boardFreq[board[i][j]]++;
            }
        }

        for (char c : word) {
            if (--boardFreq[c] < 0)
                return false;
        }

        // Step 2: Start from rarer character
        int firstCount = 0, lastCount = 0;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (board[i][j] == word[0]) firstCount++;
                if (board[i][j] == word[word.size()-1]) lastCount++;
            }
        }

        if (lastCount < firstCount) {
            reverse(word.begin(), word.end());
        }

        // Normal DFS
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (dfs(i, j, board, word, 0))
                    return true;
            }
        }

        return false;
    }

    bool dfs(int i, int j, vector<vector<char>>& board,
             string& word, int index) {

        if (index == word.size())
            return true;

        int m = board.size();
        int n = board[0].size();

        if (i < 0 || i >= m || j < 0 || j >= n ||
            board[i][j] != word[index])
            return false;

        char temp = board[i][j];
        board[i][j] = '#';

        bool found =
            dfs(i+1, j, board, word, index+1) ||
            dfs(i-1, j, board, word, index+1) ||
            dfs(i, j+1, board, word, index+1) ||
            dfs(i, j-1, board, word, index+1);

        board[i][j] = temp;

        return found;
    }
};

Time and Space Complexity

  • Time: O(m × n × 4^L)

Where:

  • m × n → possible starting points
  • L → length of word
  • 4^L → exploring 4 directions recursively

With pruning, average performance improves significantly.

  • Space: O(L)
  • Due to recursion stack
  • No extra data structures used apart from frequency array

Final Takeaways

  • Always break the problem into smaller subproblems.

  • In recursion, always handle exit/base conditions carefully.

  • Backtracking means:

    • Mark
    • Explore
    • Restore

  • Try to reduce unnecessary recursive calls using pruning.

  • Grid + word search problems → Think DFS + Backtracking first.